Drug Name Inventor

Mitch Fawcett
October 3, 2018

It seems the pharmaceutical industry has devoured all the likely names for new drugs so it is getting harder and harder to come up with new ones.

This Python program attempts to solve that problem using deep learning. A character based language model will be trained using a list of most of the existing drugs to generate new names suitable for marketing.

It assumes another Python program called LoadDrugNames has previously compiled the list of existing drug names to use for training the model. The drug list was found on the NIH Web site and contains the names of about 3,000 drugs. The data engineering that went into extracting the names from the Web site will be skipped over here.

We will begin by loading the libraries we'll need plus some functions that are provided in rnn_utils. Specifically; functions such as rnn_forward and rnn_backward.

import numpy as np
from utils import *
import random

1 - Problem Statement

1.1 - Dataset and Preprocessing

Run the following cell to read the dataset of existing drug names, create a list of unique characters (such as a-z), and compute the dataset and vocabulary size.

data = open('drugnames.csv', 'r').read()
data= data.lower()
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
drug_count = len(open('drugnames.csv').readlines())

print('There are %d drug names in the training data.' % (drug_count))
print('There are %d total characters and %d unique characters in the training data.' % (data_size, vocab_size))

There are 3047 drug names in the training data.
There are 29291 total characters and 27 unique characters in the training data.

The characters are a-z (26 characters) plus the "\n" (or newline character), which indicates the end of the drug name. In the cell below, we create a python dictionary (i.e., a hash table) to map each character to an index from 0-26. We also create a second python dictionary that maps each index back to the corresponding character character. This will help you figure out what index corresponds to what character in the probability distribution output of the softmax layer. Below, char_to_ix and ix_to_char are the python dictionaries.

char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }
ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }
print(ix_to_char)
print(char_to_ix)

{0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}
{'\n': 0, 'a': 1, 'b': 2, 'c': 3, 'd': 4, 'e': 5, 'f': 6, 'g': 7, 'h': 8, 'i': 9, 'j': 10, 'k': 11, 'l': 12, 'm': 13, 'n': 14, 'o': 15, 'p': 16, 'q': 17, 'r': 18, 's': 19, 't': 20, 'u': 21, 'v': 22, 'w': 23, 'x': 24, 'y': 25, 'z': 26}

1.2 - Overview of the model

Your model will have the following structure:

• Initialize parameters
• Run the optimization loop
  • Forward propagation to compute the loss function
  • Backward propagation to compute the gradients with respect to the loss function
  • Clip the gradients to avoid exploding gradients
  • Using the gradients, update your parameter with the gradient descent update rule.
• Return the learned parameters

**Figure 1**: Recurrent Neural Network, similar to what you had built in the previous notebook "Building a RNN - Step by Step".

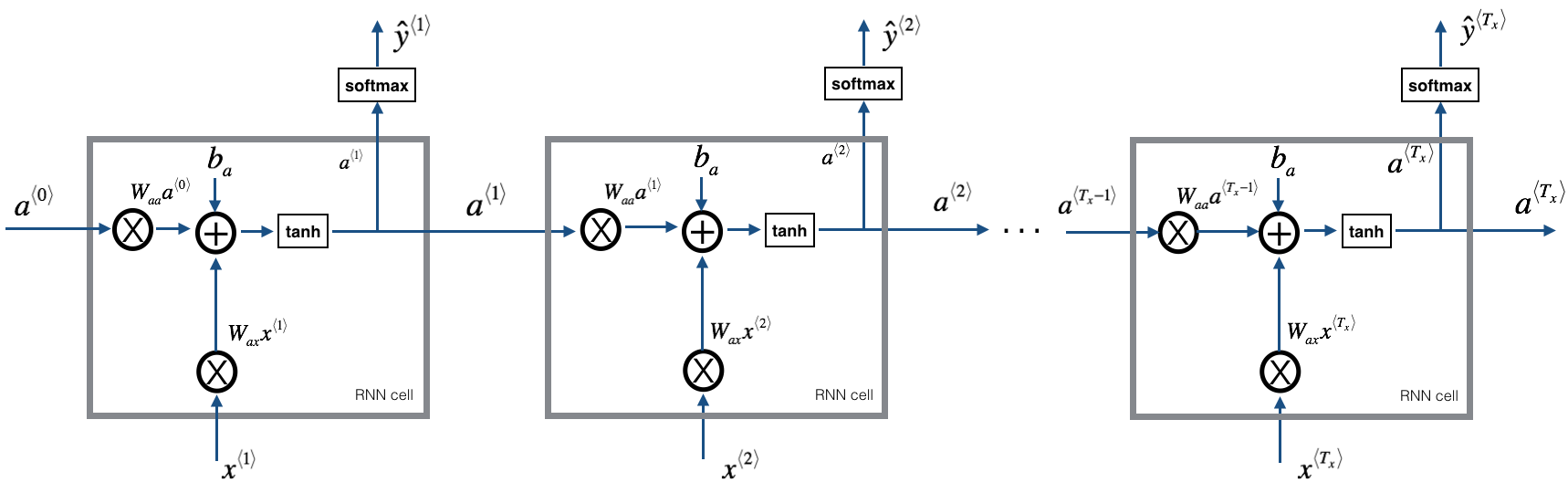
At each time-step, the RNN tries to predict what is the next character given the previous characters. The dataset $X = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle})$ is a list of characters in the training set, while $Y = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle})$ is such that at every time-step $t$, we have $y^{\langle t \rangle} = x^{\langle t+1 \rangle}$.

2 - Building blocks of the model

In this part, you will build two important blocks of the overall model:

• Gradient clipping: to avoid exploding gradients
• Sampling: a technique used to generate characters

You will then apply these two functions to build the model.

2.1 - Clipping the gradients in the optimization loop

In this section you will implement the clip function that you will call inside of your optimization loop. Recall that your overall loop structure usually consists of a forward pass, a cost computation, a backward pass, and a parameter update. Before updating the parameters, you will perform gradient clipping when needed to make sure that your gradients are not "exploding," meaning taking on overly large values.

In the exercise below, you will implement a function clip that takes in a dictionary of gradients and returns a clipped version of gradients if needed. There are different ways to clip gradients; we will use a simple element-wise clipping procedure, in which every element of the gradient vector is clipped to lie between some range [-N, N]. More generally, you will provide a maxValue (say 10). In this example, if any component of the gradient vector is greater than 10, it would be set to 10; and if any component of the gradient vector is less than -10, it would be set to -10. If it is between -10 and 10, it is left alone.

**Figure 2**: Visualization of gradient descent with and without gradient clipping, in a case where the network is running into slight "exploding gradient" problems.

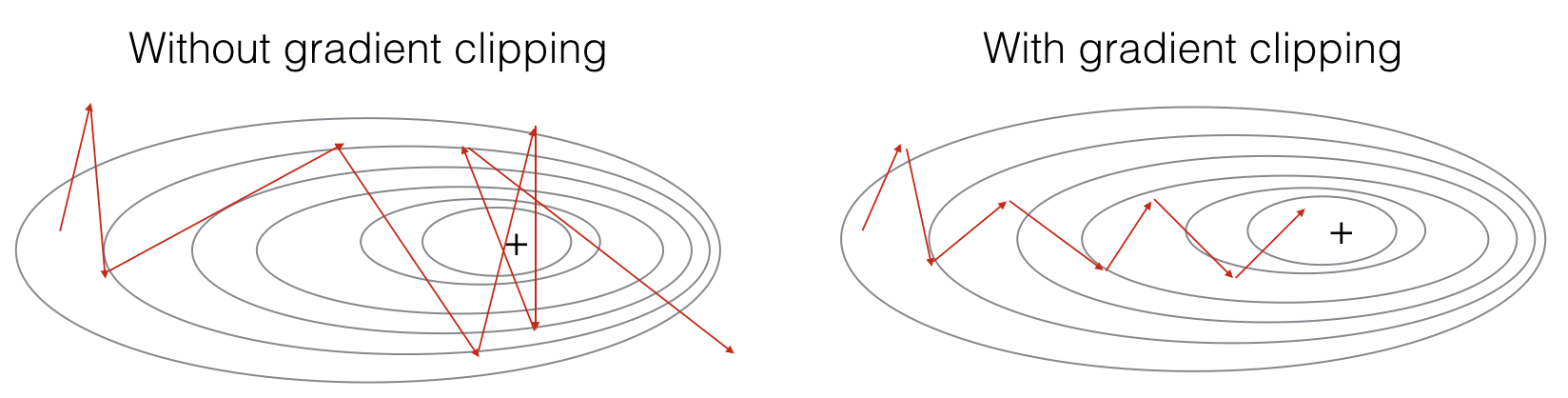
Exercise: Implement the function below to return the clipped gradients of your dictionary gradients. Your function takes in a maximum threshold and returns the clipped versions of your gradients. You can check out this hint for examples of how to clip in numpy. You will need to use the argument out = ....

### GRADED FUNCTION: clip

def clip(gradients, maxValue):
    '''
    Clips the gradients' values between minimum and maximum.
    
    Arguments:
    gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
    maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
    
    Returns: 
    gradients -- a dictionary with the clipped gradients.
    '''
    
    dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']
   
    ### START CODE HERE ###
    # clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, db, dby]. (≈2 lines)
    for gradient in [dWax, dWaa, dWya, db, dby]:
        np.clip(gradient, -1 * maxValue, maxValue, out = gradient)
    ### END CODE HERE ###
    
    gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
    
    return gradients

np.random.seed(3)
dWax = np.random.randn(5,3)*10
dWaa = np.random.randn(5,5)*10
dWya = np.random.randn(2,5)*10
db = np.random.randn(5,1)*10
dby = np.random.randn(2,1)*10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, 10)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])

gradients["dWaa"][1][2] = 10.0
gradients["dWax"][3][1] = -10.0
gradients["dWya"][1][2] = 0.2971381536101662
gradients["db"][4] = [10.]
gradients["dby"][1] = [8.45833407]

** Expected output:**

**gradients["dWaa"][1][2] **	10.0
**gradients["dWax"][3][1]**	-10.0
**gradients["dWya"][1][2]**	0.29713815361
**gradients["db"][4]**	[ 10.]
**gradients["dby"][1]**	[ 8.45833407]

2.2 - Sampling

Now assume that your model is trained. You would like to generate new text (characters). The process of generation is explained in the picture below:

**Figure 3**: In this picture, we assume the model is already trained. We pass in $x^{\langle 1\rangle} = \vec{0}$ at the first time step, and have the network then sample one character at a time.

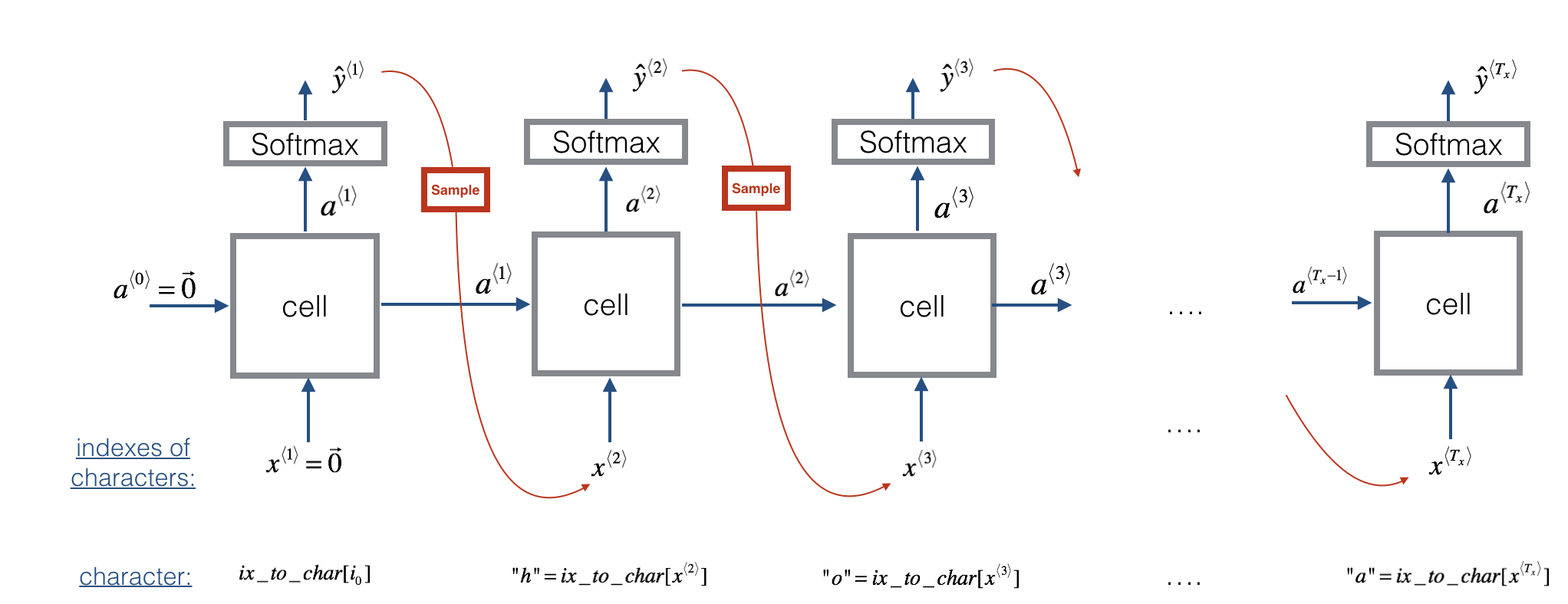
Exercise: Implement the sample function below to sample characters. You need to carry out 4 steps:

• Step 1: Pass the network the first "dummy" input $x^{\langle 1 \rangle} = \vec{0}$ (the vector of zeros). This is the default input before we've generated any characters. We also set $a^{\langle 0 \rangle} = \vec{0}$

• Step 2: Run one step of forward propagation to get $a^{\langle 1 \rangle}$ and $\hat{y}^{\langle 1 \rangle}$. Here are the equations:

$$ a^{\langle t+1 \rangle} = \tanh(W_{ax} x^{\langle t \rangle } + W_{aa} a^{\langle t \rangle } + b)\tag{1}$$$$ z^{\langle t + 1 \rangle } = W_{ya} a^{\langle t + 1 \rangle } + b_y \tag{2}$$$$ \hat{y}^{\langle t+1 \rangle } = softmax(z^{\langle t + 1 \rangle })\tag{3}$$

Note that $\hat{y}^{\langle t+1 \rangle }$ is a (softmax) probability vector (its entries are between 0 and 1 and sum to 1). $\hat{y}^{\langle t+1 \rangle}_i$ represents the probability that the character indexed by "i" is the next character. We have provided a softmax() function that you can use.

• Step 3: Carry out sampling: Pick the next character's index according to the probability distribution specified by $\hat{y}^{\langle t+1 \rangle }$. This means that if $\hat{y}^{\langle t+1 \rangle }_i = 0.16$, you will pick the index "i" with 16% probability. To implement it, you can use np.random.choice.

Here is an example of how to use np.random.choice():

np.random.seed(0)
p = np.array([0.1, 0.0, 0.7, 0.2])
index = np.random.choice([0, 1, 2, 3], p = p.ravel())

This means that you will pick the index according to the distribution: $P(index = 0) = 0.1, P(index = 1) = 0.0, P(index = 2) = 0.7, P(index = 3) = 0.2$.

• Step 4: The last step to implement in sample() is to overwrite the variable x, which currently stores $x^{\langle t \rangle }$, with the value of $x^{\langle t + 1 \rangle }$. You will represent $x^{\langle t + 1 \rangle }$ by creating a one-hot vector corresponding to the character you've chosen as your prediction. You will then forward propagate $x^{\langle t + 1 \rangle }$ in Step 1 and keep repeating the process until you get a "\n" character, indicating you've reached the end of the dinosaur name.

# GRADED FUNCTION: sample

def sample(parameters, char_to_ix, seed, max_length):
    """
    Sample a sequence of characters according to a sequence of probability distributions output of the RNN

    Arguments:
    parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b. 
    char_to_ix -- python dictionary mapping each character to an index.
    seed -- used for grading purposes. Do not worry about it.
    max_length - the maximum number of characters to use in a name

    Returns:
    indices -- a list of length n containing the indices of the sampled characters.
    """
    
    # Retrieve parameters and relevant shapes from "parameters" dictionary
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]
    n_a = Waa.shape[1]
    
    ### START CODE HERE ###
    # Step 1: Create the one-hot vector x for the first character (initializing the sequence generation). (≈1 line)
    x = np.zeros(shape = (vocab_size, 1))
    # Step 1': Initialize a_prev as zeros (≈1 line)
    a_prev = np.zeros(shape = (n_a, 1))
    
    # Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
    indices = []
    
    # Idx is a flag to detect a newline character, we initialize it to -1
    idx = -1 
    
    # Loop over time-steps t. At each time-step, sample a character from a probability distribution and append 
    # its index to "indices". We'll stop if we reach max_length characters (which should be very unlikely with a well 
    # trained model), which helps debugging and prevents entering an infinite loop. 
    counter = 0
    newline_character = char_to_ix['\n']
    

    while (idx != newline_character and counter != max_length):
        
        # Step 2: Forward propagate x using the equations (1), (2) and (3)
        a = np.tanh(np.add(np.matmul(Wax, x), np.matmul(Waa, a_prev)) + b)
        z = np.matmul(Wya, a) + by
        y = softmax(z)
        # print(y)  
        # print(np.sum(y))
        
        # for grading purposes
        np.random.seed(counter+seed) 
        
        # Step 3: Sample the index of a character within the vocabulary from the probability distribution y
        idx = np.random.choice(vocab_size, p = y.ravel())
        
        ### Note - despite the "random.choice" in the name of the above function, it is not randomly choosing
        ### a letter index.  It is choosing the letter index with the highest probability.  It will choose the 
        ### index of the element in y that has the highest value.
        
        ## print(y[idx])
        ## print(idx)        
        ## print(ix_to_char[idx])
        
        # Append the index to "indices"
        indices.append(idx)
        
        # Step 4: Overwrite the input character as the one corresponding to the sampled index        
        x = np.zeros(shape = (vocab_size, 1))
        x[idx] = 1
        
        # Update "a_prev" to be "a"
        a_prev = a
        
        # for grading purposes
        seed += 1
        counter +=1
        
    ### END CODE HERE ###

    if (counter == max_length):
        indices.append(char_to_ix['\n'])
    
    return indices

np.random.seed(2)
_, n_a = 20, 100
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}


indices = sample(parameters, char_to_ix, 0, 20)
print("Sampling:")
print("list of sampled indices:", indices)
print("list of sampled characters:", [ix_to_char[i] for i in indices])

Sampling:
list of sampled indices: [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 0]
list of sampled characters: ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', '\n']

** Expected output:**

**list of sampled indices:**	[12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 5, 6, 12, 25, 0, 0]
**list of sampled characters:**	['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'e', 'f', 'l', 'y', '\n', '\n']

3 - Building the language model

It is time to build the character-level language model for text generation.

3.1 - Gradient descent

In this section you will implement a function performing one step of stochastic gradient descent (with clipped gradients). You will go through the training examples one at a time, so the optimization algorithm will be stochastic gradient descent. As a reminder, here are the steps of a common optimization loop for an RNN:

• Forward propagate through the RNN to compute the loss
• Backward propagate through time to compute the gradients of the loss with respect to the parameters
• Clip the gradients if necessary
• Update your parameters using gradient descent

Exercise: Implement this optimization process (one step of stochastic gradient descent).

We provide you with the following functions:

def rnn_forward(X, Y, a_prev, parameters):
    """ Performs the forward propagation through the RNN and computes the cross-entropy loss.
    It returns the loss' value as well as a "cache" storing values to be used in the backpropagation."""
    ....
    return loss, cache

def rnn_backward(X, Y, parameters, cache):
    """ Performs the backward propagation through time to compute the gradients of the loss with respect
    to the parameters. It returns also all the hidden states."""
    ...
    return gradients, a

def update_parameters(parameters, gradients, learning_rate):
    """ Updates parameters using the Gradient Descent Update Rule."""
    ...
    return parameters

# GRADED FUNCTION: optimize

def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
    """
    Execute one step of the optimization to train the model.
    
    Arguments:
    X -- list of integers, where each integer is a number that maps to a character in the vocabulary.
    Y -- list of integers, exactly the same as X but shifted one index to the left.
    a_prev -- previous hidden state.
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        b --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    learning_rate -- learning rate for the model.
    
    Returns:
    loss -- value of the loss function (cross-entropy)
    gradients -- python dictionary containing:
                        dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
                        dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
                        dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
                        db -- Gradients of bias vector, of shape (n_a, 1)
                        dby -- Gradients of output bias vector, of shape (n_y, 1)
    a[len(X)-1] -- the last hidden state, of shape (n_a, 1)
    """
    
    ### START CODE HERE ###
    
    # Forward propagate through time (≈1 line)
    loss, cache = rnn_forward(X, Y, a_prev, parameters)
    
    # Backpropagate through time (≈1 line)
    gradients, a = rnn_backward(X, Y, parameters, cache)
    
    # Clip your gradients between -5 (min) and 5 (max) (≈1 line)
    gradients = clip(gradients, 10)
    
    # Update parameters (≈1 line)
    parameters = update_parameters(parameters, gradients, learning_rate)
    
    ### END CODE HERE ###
    
    return loss, gradients, a[len(X)-1]

np.random.seed(1)
vocab_size, n_a = 27, 100
a_prev = np.random.randn(n_a, 1)
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
X = [12,3,5,11,22,3]
Y = [4,14,11,22,25, 26]

loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
print("Loss =", loss)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("np.argmax(gradients[\"dWax\"]) =", np.argmax(gradients["dWax"]))
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
print("a_last[4] =", a_last[4])

Loss = 126.50397572165339
gradients["dWaa"][1][2] = 0.19470931534726388
np.argmax(gradients["dWax"]) = 93
gradients["dWya"][1][2] = -0.007773876032004454
gradients["db"][4] = [-0.06809825]
gradients["dby"][1] = [0.01538192]
a_last[4] = [-1.]

** Expected output:**

**Loss **	126.503975722
**gradients["dWaa"][1][2]**	0.194709315347
**np.argmax(gradients["dWax"])**	93
**gradients["dWya"][1][2]**	-0.007773876032
**gradients["db"][4]**	[-0.06809825]
**gradients["dby"][1]**	[ 0.01538192]
**a_last[4]**	[-1.]

3.2 - Training the model

Given the dataset of drug names, we use each line of the dataset (one name) as one training example. Every 2000 steps of stochastic gradient descent, you will sample 7 randomly chosen names to see how the algorithm is doing. Remember to shuffle the dataset, so that stochastic gradient descent visits the examples in random order.

Exercise: Follow the instructions and implement model(). When examples[index] contains one drug name (string), to create an example (X, Y), you can use this:

index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]] 
        Y = X[1:] + [char_to_ix["\n"]]

Note that we use: index= j % len(examples), where j = 1....num_iterations, to make sure that examples[index] is always a valid statement (index is smaller than len(examples)). The first entry of X being None will be interpreted by rnn_forward() as setting $x^{\langle 0 \rangle} = \vec{0}$. Further, this ensures that Y is equal to X but shifted one step to the left, and with an additional "\n" appended to signify the end of the dinosaur name.

# GRADED FUNCTION: model

def model(data, ix_to_char, char_to_ix, num_iterations = 100001, n_a = 50, drug_names = 7, vocab_size = 27):
    """
    Trains the model and generates dinosaur names. 
    
    Arguments:
    data -- text corpus
    ix_to_char -- dictionary that maps the index to a character
    char_to_ix -- dictionary that maps a character to an index
    num_iterations -- number of iterations to train the model for
    n_a -- number of units of the RNN cell
    drug_names -- number of drug names you want to sample at each iteration. 
    vocab_size -- number of unique characters found in the text, size of the vocabulary
    
    Returns:
    parameters -- learned parameters
    """
    
    # Retrieve n_x and n_y from vocab_size
    n_x, n_y = vocab_size, vocab_size
    
    # Initialize parameters
    parameters = initialize_parameters(n_a, n_x, n_y)
    
    # Initialize loss (this is required because we want to smooth our loss, don't worry about it)
    loss = get_initial_loss(vocab_size, drug_names)
    
    # Build list of all drug names (training examples).
    with open("drugnames.csv") as f:
        examples = f.readlines()
    examples = [x.lower().strip() for x in examples]
    ## some_string.partition(' ')[0]
    
    # Shuffle list of all drug names
    np.random.seed(0)
    np.random.shuffle(examples)
    
    # Initialize the hidden state of your LSTM
    a_prev = np.zeros((n_a, 1))
    
    # Optimization loop
    for j in range(num_iterations):
        
        ### START CODE HERE ###
        
        # Use the hint above to define one training example (X,Y) (≈ 2 lines)
        index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]]
        Y = X[1:] + [char_to_ix["\n"]]
        
        # Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters
        # Choose a learning rate of 0.01 - experimentation shows this to produce good results.
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate = 0.005)
        
        ### END CODE HERE ###
        
        # Use a latency trick to keep the loss smooth. It happens here to accelerate the training.
        loss = smooth(loss, curr_loss)

        # Every 2000 Iteration, generate "n" characters thanks to sample() to check if the model is learning properly
        if j % 2000 == 0:
            
            print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
            
            # The number of drug names to print
            seed = 0
            for name in range(drug_names):
                
                # Sample indices and print them
                sampled_indices = sample(parameters, char_to_ix, seed, max_length = 20)
                print_sample(sampled_indices, ix_to_char)
                
                seed += 1  # To get the same result for grading purposed, increment the seed by one. 
      
            print('\n')
        
    return parameters

Run the following cell, you should observe your model outputting random-looking characters at the first iteration. After a few thousand iterations, your model should learn to generate reasonable-looking names.

parameters = model(data, ix_to_char, char_to_ix)

Iteration: 0, Loss: 23.080744

Nkzxwtdmfqoeyhsqwasj
Kneb
Kzxwtdmfqoeyhsqwasjk
Neb
Zxwtdmfqoeyhsqwasjkj
Eb
Xwtdmfqoeyhsqwasjkjv


Iteration: 2000, Loss: 26.995978

Lgxttpananifvepns
Inaa
Ixttpamanifvepns
Laa
Ytsrananifvepns
C
Ttpananifvepns


Iteration: 4000, Loss: 25.147021

Mixstodilin
In
Ixstodilin
Mac
Ytrodilhmaxerlrarele
Da
Trodilgnaxborobomejt


Iteration: 6000, Loss: 23.882982

Onutrofilen
Lleb
Lvroran
Ol
Ytrofilen
Eb
Trogiine


Iteration: 8000, Loss: 23.601685

Mivrpram
Ine
Lytrode
Mecaerol
Ytrode
Ecagrol
Utran


Iteration: 10000, Loss: 23.292904

Mixtrofilin
Lola
Lyutoin
Mecafose
Yutranane
Ecafprecanrevelivil

Utranapiluloprasenes


Iteration: 12000, Loss: 22.876617

Miwtrocimefaxaris
Klec
Lyutofimegax
Mec
Yutpan
Daacose
Utramaon


Iteration: 14000, Loss: 22.934291

Mextrociebadulorp
Inda
Ivutode
Mecadote
Xutram
Daacota
Uutam


Iteration: 16000, Loss: 22.592878

Mivostan
Inea
Lytroen
Mecafore
Xytramepilterlocomel
Daacore
Ustdiflidseros


Iteration: 18000, Loss: 22.222472

Mivstramdin
Inda
Lytrogimed
Mec
Xytramclolyfort
Daadose
Ustaperidrestrapin


Iteration: 20000, Loss: 22.345095

Mivprofilin
Hlec
Ivtrofilin
Mec
Wutram
Caadote
Utran


Iteration: 22000, Loss: 22.072606

Mivotide
Hlec
Ivprodifen
Mec
Wutram
Caadosd
Utram


Iteration: 24000, Loss: 21.673107

Nexstram
Inda
Kytrofinam
Nec
Vutramana
Cabetrea
Utramand


Iteration: 26000, Loss: 21.851720

Mivoxide
Hlda
Iwustan
Mec
Vutran
Caacosfab
Ustaqcin


Iteration: 28000, Loss: 21.687051

Onvotofidin
Hlec
Ivovide
Ola
Vprodide
Caacose
Ustaqcinazerip


Iteration: 30000, Loss: 21.309098

Pivotral
Jged
Lxutrafene
Pefagrol
Vutramane
Daadlon
Ustarane


Iteration: 32000, Loss: 21.434713

Nextor
Hoda
Jytrofime
Nec
Vsuram
Daadose
Ustarane


Iteration: 34000, Loss: 21.357114

Powtroke
Lola
Lytrolade
Phaadir
Vostan
Egalox
Voramcin


Iteration: 36000, Loss: 21.041664

Pivoxoceine
Lola
Lxutral
Ped
Votram
Daadova
Voseogin


Iteration: 38000, Loss: 21.195486

Pivotoladin
Lofa
Lytroge
Pedadore
Votolide
Daacose
Vosemare


Iteration: 40000, Loss: 21.144732

Piustol
Lola
Mytroghene
Pefaine
Vostan
Efalovec
Voral


Iteration: 42000, Loss: 20.884818

Plutrol
Loha
Mytrol
Pedadose
Votran
Edafose
Vosenasinige


Iteration: 44000, Loss: 21.003643

Pluvoschenidrespr
Loic
Lytroephloline
Ped
Votoleglimole
Daacosc
Voscilapatapin


Iteration: 46000, Loss: 21.028819

Pluvjramane
Lmed
Lvovil
Pegadin
Votran
Efagrol
Voscindinidine


Iteration: 48000, Loss: 20.798916

Pivotoged
Mida
Mytrofene
Ped
Votran
Edacprec
Vosciflimudine


Iteration: 50000, Loss: 20.828868

Omytrol
Kida
Lyvose
Ped
Votram
Edaklon
Vosen


Iteration: 52000, Loss: 20.797979

Pivovil
Mlgabaton
Nuvosen
Pefadrol
Votranasine
Edagpred
Vosencin


Iteration: 54000, Loss: 20.736775

Plutrol
Loga
Mytrogelin
Ped
Votran
Dabatref
Voscilin


Iteration: 56000, Loss: 20.674871

Proxypan
Lola
Mytro
Pha
Votram
Ed
Voscil


Iteration: 58000, Loss: 20.699434

Phystogelline
Miga
Mytrocin
Pefadose
Votram
Edafloma
Vosenare


Iteration: 60000, Loss: 20.676948

Plustide
Lofa
Lutrofidin
Ped
Votrenasile
Dabatred
Vosenapilol


Iteration: 62000, Loss: 20.679923

Pluurofenin
Kela
Lyvosam
Ped
Votram
Daacose
Voram


Iteration: 64000, Loss: 20.602407

Phystram
Lofaacipe
Mytrofensoluline
Pefadrol
Votramar
Edakote
Voralan


Iteration: 66000, Loss: 20.654231

Plutrocilin
Khec
Luutraheprex
Peg
Votranale
Daadrol
Urodien


Iteration: 68000, Loss: 20.617454

Pnovoscaine
Kidaab
Lyustar
Ped
Votran
Daacor
Voscelcine


Iteration: 70000, Loss: 20.441042

Plustiem
Kela
Lutroephonavarin
Pef
Votran
Daadose
Triceflilphonibin


Iteration: 72000, Loss: 20.621997

Nexotolachidrene
Gelaacin
Ituspan
Ogabetil
Votranamidine
Daberol
Trochene


Iteration: 74000, Loss: 20.560270

Omytro
Hyda
Kytrofened
Olabatol
Votran
Cabcose
Urtaperidole


Iteration: 76000, Loss: 20.435749

Omytrl
Kida
Lyutra
Pha
Votran
Ed
Tricilin


Iteration: 78000, Loss: 20.591319

Olytro
Hida
Jutrogel
Oga
Votrasepole
Cabdium
Trocheridole


Iteration: 80000, Loss: 20.579818

Omytrodide
Inec
Lytrocinin
Peg
Votran
Dabetrac
Trocimine


Iteration: 82000, Loss: 20.316168

Omytrife
Kiga
Lytrolecin
Olaacin
Votran
Dabetrid
Trofletile


Iteration: 84000, Loss: 20.528730

Omytro
Inec
Lutrokide
Ogab
Votran
Cabbita
Trofem


Iteration: 86000, Loss: 20.464148

Mextrohidine
Floc
Hytrofilline
Mbbador
Votran
Cabatol
Trofilline


Iteration: 88000, Loss: 20.220764

Omytroflin
Inda
Kytrogen
Ogabetred
Vovigil
Dabesta
Trocilline


Iteration: 90000, Loss: 20.618712

Mextrofline
Gic
Hytrocilline
Mec
Votranalcat
Cabdora
Trocilline


Iteration: 92000, Loss: 20.520656

Mixotranapinidine
Flla
Grovih
Medalote
Votrandin
Cabetrac
Trogem


Iteration: 94000, Loss: 20.311747

Nexrose
Gena
Hytrofine
Ndabetrid
Vovilefa
Cabetreabe
Trofine


Iteration: 96000, Loss: 20.396666

Mextrofimine
Floc
Frustan
Mecaflol
Votochene
Cabdosa
Trofeniolol


Iteration: 98000, Loss: 20.528595

Omytrocindilol
Glec
Iutridide
Olaaglor
Vourandin
Cabesteaclone
Urogimin


Iteration: 100000, Loss: 20.202982

Omytrodine
Gifabatin
Hytrodidin
Ogabatol
Vovidil
Caberom
Trochene

Conclusion

You can see that the algorithm has started to generate plausible drug names towards the end of the training. At first, it was generating random characters, but towards the end you could see drug names with definite marketing potential.

If the model generates some non-cool names, don't blame the model entirely. This experiment had used a relatively small dataset. Training a model of the english language requires a much bigger dataset, and usually needs much more computation, and could run for many hours on GPUs.

Notes

It may seem a little confusing what this program is doing since it is outputting results while the training phase is taking place. One of the goals of this experiment is to show how the outputs of a language model can improve with longer periods of training. So the training loop (which is happening over a total of 'n' iterations) is interrupted periodically to show how the generated drug names become more reasonable the longer the training runs.

In normal practice you would train a model, monitoring the loss to assure it is decreasing, and then at some point stop. Then you would use the model by generating some output.